GCPP:Proposal-Isinglass
Puzzle Codename: Isinglass
| Contact | |
| Username: | karein |
| Additional contact info: | On Hunter as Karein, griffer13524@comcast.net, AIM: griffer13524 |
| Project forum thread: | Discussion |
Game concept
This puzzle would work for either tailor or weaving. The game is similar to Mad Virus (http://www.bubblebox.com/game/puzzle/539.htm) where the player would be dying fabric to make it the same color.
Objective
In a certain number of turns, the player would have to have made the whole game board the same color.
Gameplay
The gameplay takes place on a board made up of hexagonal squares. At the beginning of the game the each space on the board is assigned a color, and one space is designated as the starting space. The player has a limited amount of turns to make the whole playing field the same color.
On the first turn, the player selects one of the spaces adjacent to his starting space. The player’s starting space becomes that color, and that player now controls all of the contiguous spaces on the board that are of the selected square’s color. Gameplay continues with the player then selecting another space adjacent to any of the spaces he controls. After doing so, the character’s area shifts to whatever color the newly selected space is, and his area expands to contain the contiguous area. The player’s area of control would be marked by a border. The player would continue until he completes the board or runs out of turns.
After the player completes a board, he or she moves onto another, until they have played through five boards, regardless of whether they botched a board or not.
Storyboard
This is an example of a board being played. I demonstrated all of the special spaces except for holes. The area is intentionally small, an actual playing board would be much larger.
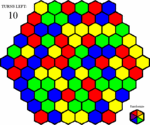
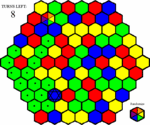
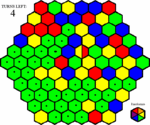
Fig. 1 - This is the layout of the puzzle. The board takes up most of the space. In the top left is a counter for the number of turns left, and in the botton right is a button allowing the player to use a turn to randomize the board.
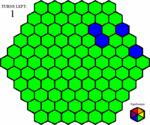
Fig.2 - John, our player, has decided to try out the new tailoring puzzle. He opens it, and is presented with a random game board. Four spaces are blinking, asking him to choose a starting square. He decides to start on the red space.
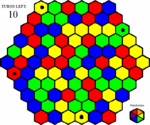
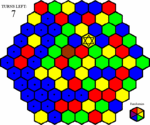
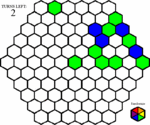
Now John has to make his first move. He sees that there is a lot of blue spaces around him, so he clicks on one of them.
John thinks he's doing pretty good, and wants to go for the bonus space which just showed up on the game board. He can't get it just yet, but if he clicks on a green space, he should be able to get it next turn.
John goes to click on the blue bonus space, but a new space catches his eye. It is a randomizing space, and he sees that clicking on the blue space would activate it. He's not too sure if it is a good idea to activate it, but he wants the bonus, and he still has quite a few turns left, so he'll give it a try.
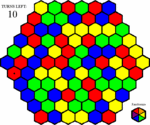
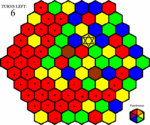
After the board settles down, John recieves a pleasant surprise. All of the spaces next to his area that came up blue after being randomized were added to his control. Not only did he get a bonus, but John is also fairly confident that he will be able to finish this board with a few turns left on the counter.
Then his attention is drawn to the new spaces on the board. A new bonus space has appeared on the board, and he sees that by clicking on a green space, he could get it the next turn. The only problem is that choosing green would also activate the new brown space. He doesn't see anyway around that yet, so all he can do is wait and hope the brown space fades away before the bonus space does. In the mean time, he clicks on a red space.
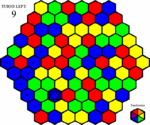
John isn't happy anymore. Not only is the first brown space still there, but a second one popped up as well. And unfortunately, he doesn't see anyway to avoid this one. Resigned to his fate he clicks on a yellow space.
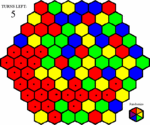
John doesn't gain any yellow territory, and none of his spaces change color. Since he activated a brown space, he lost ten to twenty percent of his spaces. All of the spaces are taken from the edges. But much to his surprise, John sees that his area is much smaller than that. Because part of his previous area was severed from the area with his starting space in it, he lost all of that area as well. The bonus space dissapeared as well, along with the first brown space. With half of his turns gone, John is beginning to get worried. He considers randomizing, but figures that will only make things worse, so he clicks on a green space.
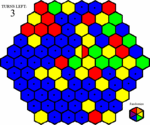
John sees the dual space appear and figures that its the only way he'll be able to finish the board and avoid a penalty. He clicks a blue space to get within range...
Clicks on the dual space...
And watches his area explode in size. He notices that not only did he gain the red and yellow squares adjacent to his area, but also the red spaces which were adjacent to yellow spaces next to his area. (His area is while because I didn't have a good way to show the two colors.) Even though he only has two turns left, John is confident as he clicks on a green space...
And then a blue space...
And completes the board just in time.
Scoring
The player would be scored for the number of spaces they gain on each turn. Passing certain thresholds could give different scores of “good,” “excellent” etc. for surpassing certain levels, the player would recieve bonuses, called clear bonuses (the "c" in the equation below).
After completing five boards, the following equation would be used to figure the score.
<math>4(v+w+x+y+z)+2(b-r)+c</math>
- v,w,x,y,z are the number of turns remaining on each board. If the player botches a board, the score for that board is -2.
- b is the number of bonus spaces acquired.
- r is the number of randomizations that occured, not counting random spaces.
- c is the clear bonuses. To recieve a clear bonus, the player would have to have an area size over ten spaces. If the player doubles their area in a single turn, then they recieve one clear bonus point.
- a score of 39 or under would be basic labor.
- a score of 40 to 79 would be skilled labor.
- a score of 80 or higher would be expert labor.
Variability
Each board would be randomly generated, so no two games would be alike.
The first variation would be the bonus spaces mentioned above. These would appear for a single turn, and then disappear.
Some levels may use holes, where there is no color, so that the character has to work around them to complete the puzzle. The spaces would only change the shape of the board.
Another bonus piece could allow characters to expand into two colors in one turn. These would be represented by spaces that either shifted from color to color, or were split down the middle. For the turn after, the characters space would mimic the dual space. These spaces would be generated at the start of the level, and they could either disappear after a set number of turns, or last for the whole level.
Some pieces might cause the player to lose control of some of his or her area. These could be represented as a brown color. If the player activated a space adjacent to the space, part of their area would be randomized and lost. These spaces would appear at random and last from one to three turns.
Another piece could randomize the rest of the board. This too would be activated by claiming a space adjacent to it. This piece could be good or bad, depending on the board. These spaces would appear at random and last from one to three turns.
The last piece would give the player another turn. This too would be activated by claiming a space adjacent to it. These spaces would appear at random and last from one to three turns.
There is a 15% chance that a special space will appear on any given turn. If one does, there is a 40% chance it will be a bonus space, 30% that it will be a brown space, 20% it will be a randomize space, and 10% it will be a n extra turn space.
At higher levels, the player would be given a choice of several starting spaces, allowing them to use strategy in deciding which space would allow them to complete the board. Not every starting space would necessarily have to be solvable, but at least one would have to have a solution.
End criteria
When the playercompletes five boards the session ends.
Difficulty scaling
Novice and easy boards are simpler. They have fewer spaces, somewhere between 150 and 200, and fewer special spaces to worry about. The only special spaces introduced would be holes and bonus spaces. There would also be fewer colors, most likely four to start. The number of turns would start at twenty and count down from there after each round.
Intermediate boards would have more spaces, between 200 and 250, and would introduce dual bonus spaces and multiple starting spaces. They would also add a color, increasing the total to five. As more of these boards are completed, the number of turns would decrease. The number of turns would start at twenty-four and count down from there after each round.
Expert levels would increase the number of spaces to anywhere above 250. They would introduce brown spaces, and possibly add one or two more colors, and larger holes. The number of turns would start at thirty and count down from there after each round.
Crafting type
Tailoring. Could also be used for weaving.
Known problems
If you find one, post in the forum below.
Notes
Images
- Sampleboards.GIF
The hexagonal board type is only possible layout. It could also be rectangular for example.
Three boards using hexagon pieces.
Three boards using square pieces.
Three boards using triangle pieces.
Three rectangular boards using hexagon pieces.
Three rectangular boards using triangle pieces.
Three rectangular boards using square pieces. Note that the easiest of these boards is the same as the easiest in the other square piece boards above.
