GCPP:Proposal-Hoki
Puzzle Codename: Hoki
| Contact | |
| Username: | Benmiff |
| Additional contact info: | On Sage as Farnoth, email as benmiff@hotmail.com |
| Project forum thread: | http://forums.puzzlepirates.com/community/mvnforum/viewthread?thread=72868 |
Game concept
A hexagonal variant of tetris but with pieces being droppable from all 6 sides and the objective being to place certain pieces into certain spaces. Designed to be a scribing puzzle to create maps (and books once implemented.)
Objective
Place pieces by "dropping" them from the 6 sides of the board. The core thing to achieve is to ensure that the landmarks are placed into the right spaces outlined on the grid.
Gameplay
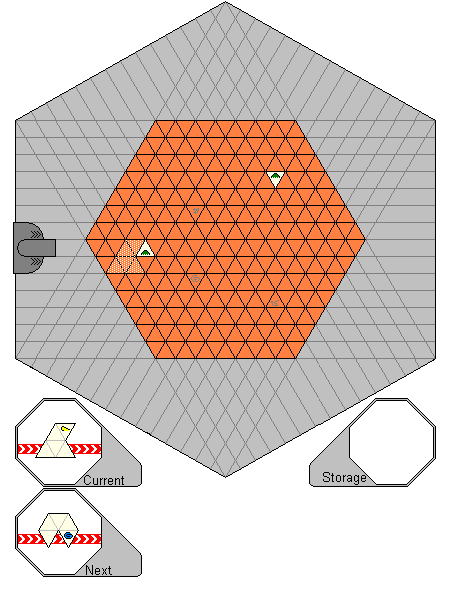
At the start, the player will have an 7 x 7 x 7 hexagonal grid. Upon this grid will be placed two islands (which are placed at random, with the constraints of not being able to be in the same row, or within two rows of the edge of the board.) They will also have an empty storage box, as well as a current piece box and a next piece box. (The next piece box and the current piece box will have one of the randomly chosen pieces on them.) In addition, a variable number of spaces on the board will have "outlines" of landmarks on them, which are to be filled with the appropiate tiles on pieces during the game. These outlines are again positioned randomly, but are also constrained by rules. An outline cannot be placed so that it is adjacent, either by an edge or by a corner, to another outline or to an island. In addition, no outline can be placed in the row nearest any of the edges. The following image shows a game board at the start :-
There are two guides to where a piece will land when "shot" from the launcher (the grey thing on the left-hand-side). (The launcher can be moved around all 6 edges of the board, and pieces can be rotated (but not flipped).) The first is in the current and next piece boxes, with the red arrow showing which side will come out of the launcher first as well as giving an alignment to it. The second is the lighter shade over the area in which the piece would land. Each piece is "shot", and then continues until it either hits another piece on the board, or it reaches the other side of the board (in which case it is considered wasted, which is penalised.) When a piece is shot, the piece in the next box is moved into the current box, and a new piece is randomly chosen for the next piece box. The game then continues in this fashion until all the outlines are filled with landmarks.
A player can booch the game in two ways. The first is by placing a piece that does not fit onto the game board. The second is by filling any outline with a piece that does not have the correct landmark on it.
The following shows all of the standard pieces (without any landmarks on them; in game, each piece will have one landmark on it somewhere.)
Scoring
There are a number of varying methods of attaining (and losing) points in scribing, some of which are dependant on particular pieces and some of which are not. The following gives a points total (which can then be considered at the end of the board when rating how well the puzzle was performed.) Please note that a lot of this scoring is for special pieces which are further explained in variability.
Basic Formula.
A basic amount of points is awarded at the end of the board according to the following formula:-
OA x OP x FA x (20 + (250 / PP) + CA)
where
OA is Outlines Available (the number of outlines that can be randomly chosen between when randomly choosing which outline each outline space will have.) OP is Outlines Placed (the number of outlines placed upon the board.) FA is Fill Adjustment PP is Pieces Placed (the number of pieces placed upon the board in the process of doing that board.) CA is Combo Adjustment (see Combos, further on.)
Embellishments.
Embellishments add a varying number of points to the base score at the end of the board depending on type and quantity, according to the final formula :-
SEV x QM
where
SEV is Sum of Embellishment Values (the sum of the values for the completed embellishments) QM is Quantity Multiplier (the multiplier value for the number of completed embellishments.)
Embellishment Values are:-
Here Be Monsters – 250 pts Sea Monster – 750 pts Ship – 1500 pts Compass – 2500 pts
Quantity Multipliers are:-
1 Embellishment placed – x 1 2 Embellishments placed – x 1.2 3 Embellishments placed – x 1.5 4 Embellishments placed – x 2
Splashdowns.
These are added to the basic score at board completion. Each splashdown is scored according to the number of additional pieces that are placed when a Typhoon piece is placed (the additional pieces being the pieces that appear in all the surrounding spaces if those spaces are empty.). No points are awarded for the first 7 additional pieces placed; the next 3 additional pieces placed give 100 pts each, and then the final piece gives 450 pts. (I am aware that there is still one additional space in which a piece could be placed; however, since this space would always be filled when the typhoon is placed since the piece must collide with another piece to be placed, there is no need to give it a points value.)
Driftwood.
At board end, the number of driftwood pieces left intact are counted, and a sum of points added to the score based upon this :-
1 Driftwood remaining – 500 pts 2 Driftwood remaining – 1000 pts 3 Driftwood remaining – 2000 pts 4 Driftwood remaining – 4000 pts etc.
Combos.
Combos are awarded by filling it outline spaces (correctly) consecutively. These change the value of CA (which begins at 0) depending on the length of the combo for each combo by adding the combo modifier. The combo modifiers are :-
x 2 combo - +1 combo modifier x 3 combo - +2 combo modifier x 4 combo - +4 combo modifier x 5 combo - +6 combo modifier x 6 combo - +9 combo modifier x 7 combo - +12 combo modifier x 8 combo - +15 combo modifier x 9 combo - +20 combo modifier x 10 combo - +25 combo modifier
Further combos beyond x 10 have a combo modifier of the previous combo + 5. (For example, a combo chain of x 22 would be +85.)
Inkblots
An inkblot can give a bonus or a penalty to the final score, dependant on whether or not they were successfully wasted. A successfully wasted inkblot adds its points value to your score, but if the inkblot is not wasted (i.e. it is placed), then the points value is deducted from your final score as a penalty instead.
Small inkblot – 200 pts value Large inkblot – 500 pts value
Fill Adjustment
The value of Fill Adjustment is dependant on whether or not the pieces you place form a constant (or two constant) blocks, without any spaces completely surrounded by placed pieces. For this to be calculated, at board end each empty space is checked to see if it is possible to trace a path from it to any edge of the board, while travelling on via empty spaces are on passing through the 3 sides of the space (rather than through corners). Each space that this cannot be done for is considered abandoned. Once this counting is done, the FA is calculated by the following formula:-
1 – (A x 0.01)
where
A is the number of abandoned spaces
Wasted
A penalty is applied to the final score for wasting pieces. Wasting is where a piece is used but does not end placed; rather, it reaches the other side of the board and is removed from the puzzle. The penalty for wasting pieces is a fixed quantity which is deducted from the final score.
1 piece wasted – 250 pts penalty 2 pieces wasted – 500 pts penalty 3 pieces wasted – 1000 pts penalty 4 pieces wasted – 2000 pts penalty etc.
Example
The following is just an example to demonstrate how the final score would be calculated with a sample board.
The board ended with 8 outlines placed, and the outlines being randomly chosen from a choice of 6 outlines. There were 28 pieces placed during the puzzle, with two combos being made, one of a length of 2 and the other of 3. There were 8 abandoned spaced left at the end of the puzzle. 1 large inkblots and 2 small inkblots were wasted; 1 other large inkblot was placed. Apart from the inkblots, 2 other pieces were wasted. At the puzzle’s end, 2 driftwood pieces were still placed and intact, and during the puzzle, 2 typhoon pieces were used, the first filling 8 additional pieces and the second 11.
The following calculations show how the final score is produced :-
Fill Adjustment is 1 – (8 x 0.01) which equals 0.92
Points added for wasted inkblots are (1 x 500) + (2 x 200) which equals 900
Points deducted placed inkblots are (1 x 200) which equals 200
Points deducted for wasting pieces are 500 pts
The combo adjustment is 0 + 2 + 1 which is 4
Points added for driftwood are 1000
Points added for splashdown are 100 for the first and 750 for the second (total 850)
The base score from the basic formula is 6 x 8 x 0.92 x (20 + (250 / 28) + 4) which is 14.92 x 32.929 which is 491.3.
The final score is 491.3 + 900 – 200 + 1000 + 850 – 500 which is 2541.3
Variability
Variability is ensured in a number of ways. The first is that as players improve, they will be given an increase in the choice of landmarks available to the puzzle to choose. The second is that there is a wide variety of special pieces, shown below :-
The pieces act as follows :-
The driftwood piece acts like a standard 2-tile piece in all respects except two. Firstly, if it is still on the board intact at the end of that board, then you get points (see Scoring for details on how much and how multiple driftwoods effect each other.) However, a driftwood is “destroyed” (removed from the board) should another piece be pushed towards it and hit it, where hitting it is where the piece would continue into the space occupied by either of the driftwood’s tiles were they not there. In this case, the piece hitting it does continue into the space left by the driftwood’s destruction until it hits something else.
The blotter piece mostly acts like a standard piece as well until it hits something. The only limitation is that they cannot be rotated like other pieces; rather, the side bordering the red area is always the side that enters the board first. When a blotter hits something, however, any tiles in the red area are removed from the board, along with the blotter itself. The only exception is filled outlines.
The inkblots act like standard pieces. However, the aim is to waste them rather than placing them. Should you waste an inkblot, you get points (with more for the large inkblot.) However, if you place an inkblot, then you get penalised points instead (again, with more for the large inkblot.)
Finally, the typhoon piece acts as a normal piece until it hits something. At that point, any space in the blue area around it that does not have a tile in it is filled with a plain ocean tile. These additional tiles also award points in the form of a splashdown, should sufficient tiles be placed.
The third, and final way, that variability is ensured is through the use of "embellishments". Standard pieces are the only pieces that can have embellishments on them; these embellishments are somewhat similar in nature to the manoeuvre tokens in carpentry, in that by placing them so that they become one cohesive whole shape, you get some points awarded. Embellishments cannot be placed on the same tile as an outline. There are 4 embellishments, which are all the same shape when completed (the shape is the same as the standard hexagon piece.) Each embellishment can be split into two or three parts. The following image shows the embellishments, both in their complete form and in their parts :-
As seen, the Here Be Monsters and Sea Monster embellishments are split into 2 pieces, where as the Ship and Compass are split into 3 pieces. The chance of a piece of an embellishment appearing on a piece is 1 in 3; when an embellishment is chosen to appear, each piece of Here Be Monsters and Ship has a 3 in 25 chance, where as each piece of Sea Monster and Compass has a 2 in 25 chance. However, a piece, once placed on the board, cannot be randomly chosen again (i.e. if you place all your embellishments, you will get each segment at most only once); in addition, if the piece itself can only have a 2-tile or 3-tile piece of an embellishment chosen on it, then the other embellishment pieces cannot be chosen. (There are also pieces that cannot take either 2-tile or 3-tile pieces, but those just do not get the 1 in 3 chance to have an embellishment on them.) An embellishment, when placed on a piece, must have its cut edges (the edges that need to meet up with other pieces of the embellishment) on the side of the piece.
If an embellishment is completed, then points are awarded for it. (See scoring for details.)
The following shows what pieces can hold what embellishments :-
Can hold 2 and 3-part pieces :- Vee, Gem, Arrow, Trapezium, El, Reversed El, Heart, Boomerang, Chair, Reversed Chair, Can hold only 2-part pieces :- Hexagon, Diamond, Reversed Diamond, Fork, Bit* Can hold only 3-part pieces :- Triangle, Cross, Cannot hold either 2 or 3-part pieces :- Any special piece
- The bit could hold a 3-part piece if it wasn’t for the requirement for all pieces to have an outline; as such, there in not enough space for the 3-part piece to be placed.
End criteria
The puzzle is ended either by booching it, or when all the outlines have been filled with the correct landmarks.
Difficulty scaling
Difficulty scales by the introduction of new bonus pieces and embellishments, as well as by the increase in the number of outlines placed on the board and the variety of landmarks from which the game can choose. (At the start, players will only have 3 landmarks available; by the higher levels, this will increase to six.)
Crafting type
Scribing. (This will be a new crafting puzzle for the creation of charts, and also books when they are produced. (They are currently on The List, so they should be implemented at some point.))
Known problems
May still be a difficulty in knowing where a piece will land on a board when fired from the launcher (although I have taken steps to try and rectify this.)
May be harder to control through the keyboard.
The outline tiles are slightly more difficult to differentiate when using a protan colour blindness test.
Notes
I have currently designed two additional things that should be useful for the game (espescially when it comes to coding.) These are the probabilities of recieving each piece in the game, and also suggested controls for playing the game.
Piece probability is as follows :-
Triangle - 0.0366 Hexagon - 0.0586 Diamond - 0.0769 Vee - 0.0403 Gem - 0.0696 Arrow - 0.0733 Trapezium - 0.0769 Cross - 0.055 El - 0.0293 Reversed El - 0.0293 Heart - 0.0696 Boomerang - 0.0733 Chair - 0.0256 Reversed Chair - 0.0256 Fork - 0.0586 Bit - 0.0293 Driftwood - 0.0256 Blotter - 0.0330 Typhoon - 0.0330 Small Inkblot - 0.0440 Large Inkblot - 0.0366
The (suggested) controls are as follows :-
For mouse:-
Use current piece – left click, Rotate piece – mouse wheel, Move shooter – move mouse itself (have the shooter be where the cursor is), Swap pieces from storage and current boxes – right click.
For the keyboard, I can see controls being somewhat more difficult to use, if only because it’s less simple.
Use current piece – space bar, Rotate piece – S and D, Move shooter – left and right arrows, Swap piece from storage and current boxes – A.
Images
The following are the outlines of landmarks that will go on the board, as well as the landmark tiles themselves. In addition, there is the two islands tiles that are used during the game:-
(Storyboard is still being made.)